Improve Your Understanding of College Level Statistics Problems
Is the correct statement that the data are discrete because the data can only take on specific values.
A Finite final consists of 50 multiple choice questions. If each question has 5 choices and 1 right answer, find the probability that a student gets an A (i.e. 45 or better) by purely guessing on each question.
A Finite final consists of 50 multiple choice questions. If each question has 5 choices and 1 right answer, find the probability that a student gets an A (i.e. 45 or better) by purely guessing on each question.
Assume that when adults with smartphones are randomly selected, 48% use them in meetings or classes. If 25 adult smartphone users are randomly selected, find the probability that exactly 16 of them use their smartphones in meetings or classes.
Assume that when adults with smartphones are randomly selected, 48% use them in meetings or classes. If 25 adult smartphone users are randomly selected, find the probability that exactly 16 of them use their smartphones in meetings or classes.
Assume that when adults with smartphones are randomly selected, 48% use them in meetings or classes. If 25 adult smartphone users are randomly selected, find the probability that exactly 16 of them use their smartphones in meetings or classes.
Assume that when adults with smartphones are randomly selected, 48% use them in meetings or classes. If 25 adult smartphone users are randomly selected, find the probability that exactly 16 of them use their smartphones in meetings or classes.
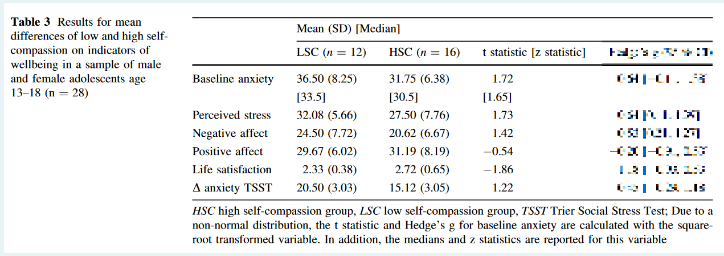
Which of the following statements is correct?
a.) With a larger sample, the mean differences examined here would increase (all other parameters remaining the same).
b.) If the standard deviations of the variable "Δ anxiety TSST" in both groups were smaller than those reported here, the t-value for the mean comparison of these variables would be larger (all other parameters being equal).
c) If, in addition to male and female adolescents, adolescents of diverse genders had also been interviewed, the t-test would no longer have been applicable. i
.e.) If it turned out that some questionnaires were incorrectly scored and the mean values for perceived stress in the group of high self-compassion were greater than 27.50, this would increase the t-value for the comparison of means (all other parameters being equal ). e.
d) To compare negative and positive affect within the group of people with low self-compassion, a one-sample t-test would be used.

Which of the following statements is correct?
a.) With a larger sample, the mean differences examined here would increase (all other parameters remaining the same).
b.) If the standard deviations of the variable "Δ anxiety TSST" in both groups were smaller than those reported here, the t-value for the mean comparison of these variables would be larger (all other parameters being equal).
c) If, in addition to male and female adolescents, adolescents of diverse genders had also been interviewed, the t-test would no longer have been applicable. i
.e.) If it turned out that some questionnaires were incorrectly scored and the mean values for perceived stress in the group of high self-compassion were greater than 27.50, this would increase the t-value for the comparison of means (all other parameters being equal ). e.
d) To compare negative and positive affect within the group of people with low self-compassion, a one-sample t-test would be used.
Find the values of x for which the series converges.
Find the sum of the series for those values of x.
Find the sum of the series for those values of x.
When Sam goes to a restaurant, he always tips the sener $2 plus 10% of the cost of the meal. If Sam's distribution of meal costs has a mean of $9 and a standard deviation of $3, what are the mean and standard deviation of the distribution
A customer organization that evaluates new automobiles customarily reports the
number of major defects in each car examined. Let ܺ denote the number of major
defects in a randomly selected car of a certain type. The cdf of ܺ is as follows:
= (ݔ)ܨ
ە
ۖ
ۖ
۔
ۖ
ۖ
ۓ
0 if ݔ > 0
0.06 if 0 ≤ ݔ > 1
0.19 if 1 ≤ ݔ > 2
0.39 if 2 ≤ ݔ > 3
0.67 if 3 ≤ ݔ > 4
0.92 if 4 ≤ ݔ > 5
0.97 if 5 ≤ ݔ > 6
1 if 6 ≤ ݔ
Calculate the following probabilities directly from the cdf.
a. ܲ(ܺ = 2)
b. ܲ(ܺ > 3)
c. ܲ(2 ≤ ܺ ≤ 5)
d. ܲ(2 < ܺ < 5)
A customer organization that evaluates new automobiles customarily reports the
number of major defects in each car examined. Let ܺ denote the number of major
defects in a randomly selected car of a certain type. The cdf of ܺ is as follows:
= (ݔ)ܨ
ە
ۖ
ۖ
۔
ۖ
ۖ
ۓ
0 if ݔ > 0
0.06 if 0 ≤ ݔ > 1
0.19 if 1 ≤ ݔ > 2
0.39 if 2 ≤ ݔ > 3
0.67 if 3 ≤ ݔ > 4
0.92 if 4 ≤ ݔ > 5
0.97 if 5 ≤ ݔ > 6
1 if 6 ≤ ݔ
Calculate the following probabilities directly from the cdf.
a. ܲ(ܺ = 2)
b. ܲ(ܺ > 3)
c. ܲ(2 ≤ ܺ ≤ 5)
d. ܲ(2 < ܺ < 5)
Which of the following quantity remains constant during the uniform circular motion?
1. A sample is chosen randomly from a population model that was strongly skewed to the right with m =145 and s =100 .
a. If we draw a random sample of n = 1000 from this population, what will be the shape of the histogram based this sample? What would be your best guess of mean and standard deviation of this sample?
b. If we draw 10,000 samples of size n = 1000 from this population, what will be the shape of the histogram of the sample means. What would be your best guess of sample mean and sample standard deviation of the distribution represented by this histogram?
a. If we draw a random sample of n = 1000 from this population, what will be the shape of the histogram based this sample? What would be your best guess of mean and standard deviation of this sample?
b. If we draw 10,000 samples of size n = 1000 from this population, what will be the shape of the histogram of the sample means. What would be your best guess of sample mean and sample standard deviation of the distribution represented by this histogram?
Find the period of a 100ft building with special steel moment frames
Review of Bronfenbrenner's Ecological Systems Theory essay
When we take from . Then the ranks are and lets take the test-statistic,
If we look at to see if , does the rank change?
For example is then correspond to ?
If we look at to see if , does the rank change?
For example is then correspond to ?
How do I know if a Binomial model is appropriate?
I have a question which is about the number of weeks out of 5 in which an event occurs. I have a frequency table with a sample of 40 - with and freq, 2,7,11,12,6,2.
I have worked out the unbiased population mean and estimate - but then I'm not sure whether binomial what I need or not? I have to decide if a bionomial model is appropriate.
I can see that the data is discrete but its not binary like "event happens" or "event does not happen". It seems relatively symmetrical - and almost normally distributed? I'm not really sure how to work this out? Is a binomial model right or not?
I have a question which is about the number of weeks out of 5 in which an event occurs. I have a frequency table with a sample of 40 - with and freq, 2,7,11,12,6,2.
I have worked out the unbiased population mean and estimate - but then I'm not sure whether binomial what I need or not? I have to decide if a bionomial model is appropriate.
I can see that the data is discrete but its not binary like "event happens" or "event does not happen". It seems relatively symmetrical - and almost normally distributed? I'm not really sure how to work this out? Is a binomial model right or not?
1. Twenty plants werer randomly selected from a normal population of palm trees to measure their height. the sample mean of the height was found to be 5 m
a. Check if there is any significant difference between the sample mean and a population mean of 6 m with standard deviation of 2 m
b. Below is a plant of residuals versus fits after a straight –line model was used on data for y= sale price of home and X = square foot area of home
1. Twenty plants werer randomly selected from a normal population of palm trees to measure their height. the sample mean of the height was found to be 5 m
a. Check if there is any significant difference between the sample mean and a population mean of 6 m with standard deviation of 2 m
b. Below is a plant of residuals versus fits after a straight –line model was used on data for y= sale price of home and X = square foot area of home
Perform hypothesis test for population mean It is claimed that average rice production by Company2 is 209,500 cwt (Company2 = 209500.0). Test this claim using a hypothesis test at 1% level of significance.
My answer: Null = 209500.0 alternative = .01
I'm being told that these my answers are not correct. I have no idea why. Any help would be appreciated!
My answer: Null = 209500.0 alternative = .01
I'm being told that these my answers are not correct. I have no idea why. Any help would be appreciated!