A family of cubic functions have zeros of -2 and 4 \pm \sqrt{7}.
Judith McQueen
Answered question
2021-12-07
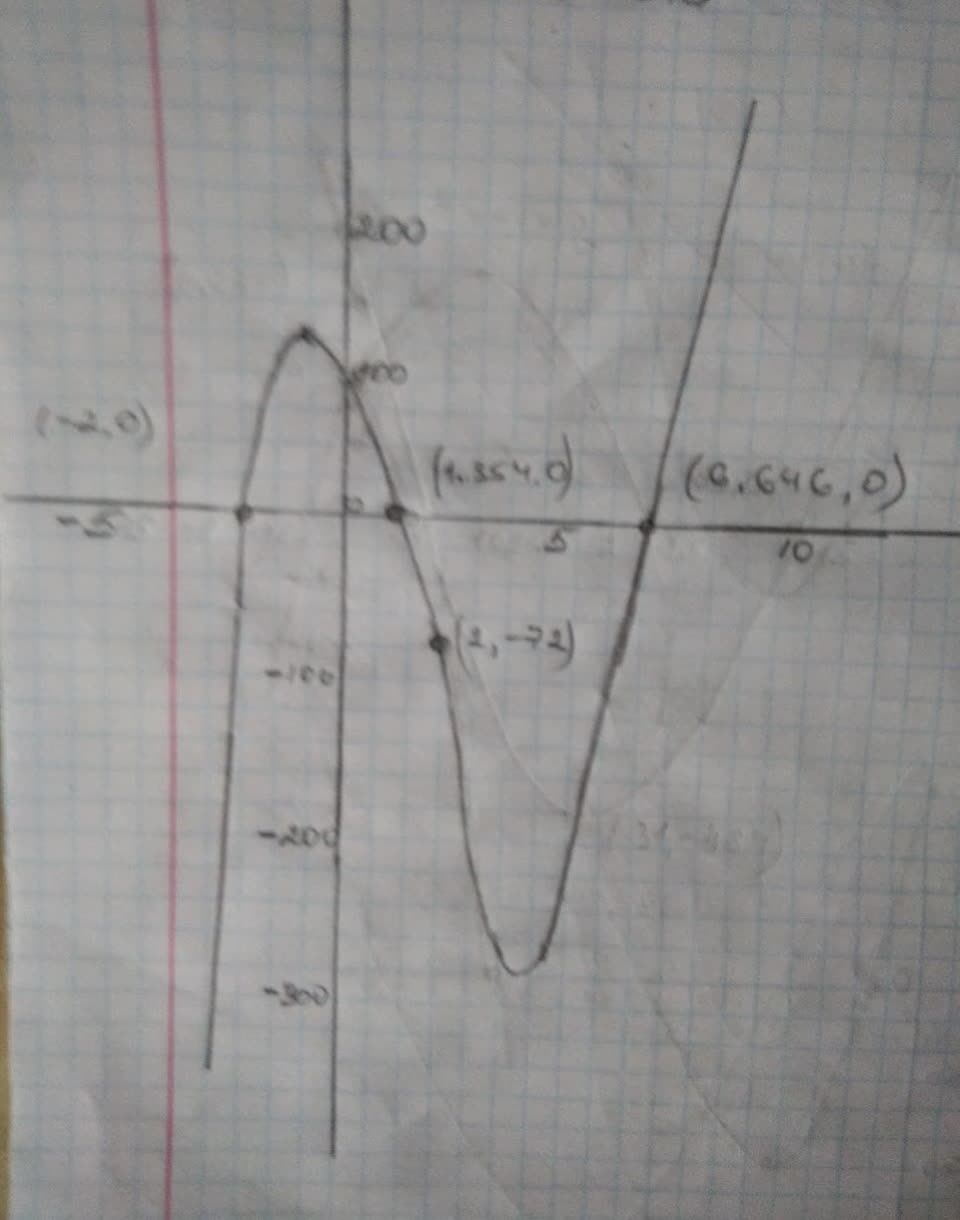
4) Write the equation ofthe family of cubic Functions in factored form. The equation may contain a ‘non-factorable quadratic but should contain no radicals. Show your work,
b) Write the equation for the member which goes through the point (2, -72). Show vour work,
c) Describe the end behaviour for the member in b).
Answer & Explanation
Ana Robertson
Beginner2021-12-08Added 26 answers
Step 1
Family of cubic functions that have the roots a,b and c is
Given roots are:
(a)
Step 2
(b) Substitute
For cubic equation which goes through point (2, -72) substitute
we get,
The graph
the three roots
New Questions in Algebra I
Find the volume V of the described solid S
A cap of a sphere with radius r and height h.
V=??
Whether each of these functions is a bijection from R to R.
a)
b)
c)
?In how many different orders can five runners finish a race if no ties are allowed???
State which of the following are linear functions?
a.
b.
c.
d.Three ounces of cinnamon costs $2.40. If there are 16 ounces in 1 pound, how much does cinnamon cost per pound?
A square is also a
A)Rhombus;
B)Parallelogram;
C)Kite;
D)none of theseWhat is the order of the numbers from least to greatest.
,
,
,
Write the numerical value of
Solve for y. 2y - 3 = 9
A)5;
B)4;
C)6;
D)3How to graph ?
How to graph using a table?
simplify
How to find the vertex of the parabola by completing the square ?
There are 60 minutes in an hour. How many minutes are there in a day (24 hours)?
Write 18 thousand in scientific notation.