Important Questions of Mensuration: Quantitative Aptitude Mensuration is one the toughest topic of quantitative aptitude section. The only thing is it
Tazmin Horton
Answered question
2021-01-04
Answer & Explanation
Ian Adams
Skilled2021-04-21Added 163 answers
Examples with Solution
Example1: What will be the area and perimeter of triangular plot whose sides are 17 m, 8m and 15m long?
Solution: Firstly, we will check which kind of triangle it is. Since,
Therefore, given triangle is a right angle triangle with: Hypotenuse 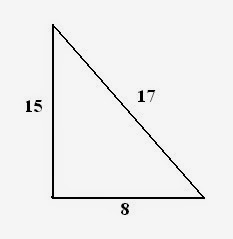
Next thing we need is: Formula of Area and perimeter Area of triangle
Also, Perimeter
Example2: What will be the area of equilateral triangle whose side is 4 cm.
Solution: Very simple question. You just need formula of area of equilateral triangle ( Equilateral triangle whose sides are equal) 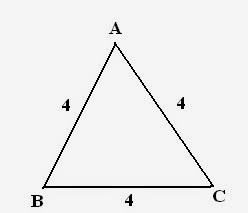
Area of equilateral triangle
Example3: The radius of a circle is 6cm. What is radius of another circle whose area is 36 times that of first?
Solution: We know that, Area is directly proportional to square of radius
Example4: One brick measures
Solution: Obviously, Number of bricks = (Total volume of wall) / (volume of 1 brick)
Note: Units should be same
Number of bricks
Example5: Surface area of cube is
Solution: Surface area of cube 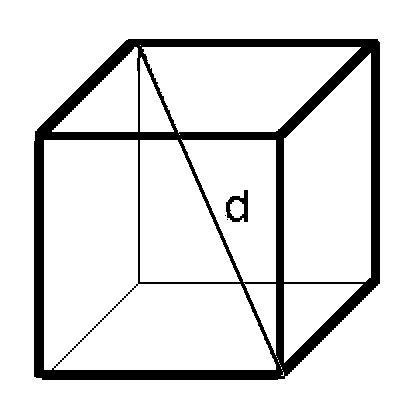
Diagonal
New Questions in High school geometry
The distance between the centers of two circles C1 and C2 is equal to 10 cm. The circles have equal radii of 10 cm.

A part of circumference of a circle is called
A. Radius
B. Segment
C. Arc
D. SectorThe perimeter of a basketball court is 108 meters and the length is 6 meters longer than twice the width. What are the length and width?
What are the coordinates of the center and the length of the radius of the circle represented by the equation ?
Which of the following pairs of angles are supplementary?
128,62
113,47
154,36
108,72What is the surface area to volume ratio of a sphere?
An angle which measures 89 degrees is a/an _____.
right angle
acute angle
obtuse angle
straight angleHerman drew a 4 sided figure which had only one pair of parallel sides. What could this figure be?
Trapezium
Parallelogram
Square
RectangleWhich quadrilateral has: All sides equal, and opposite angles equal?
Trapezium
Rhombus
Kite
RectangleKaren says every equilateral triangle is acute. Is this true?
Find the number of lines of symmetry of a circle.
A. 0
B. 4
C. 2
D. InfiniteThe endpoints of a diameter of a circle are located at (5,9) and (11, 17). What is the equation of the circle?
What is the number of lines of symmetry in a scalene triangle?
A. 0
B. 1
C. 2
D. 3How many diagonals does a rectangle has?
A quadrilateral whose diagonals are unequal, perpendicular and bisect each other is called a.
A. rhombus
B. trapezium
C. parallelogram