Important questions of Geometry for SSC CGL Tier I In my previous session, I have discussed some concepts related to triangles. Today I will discuss s
Reeves
Answered question
2021-02-16
Answer & Explanation
Ian Adams
Skilled2021-04-16Added 163 answers
Important Examples
Example1: ABCD is a cyclic quadrilateral. AB and CD are produced to meet P. If angle ADC =
Solution: First step: Make an appropriate figure using statements provided in questions.
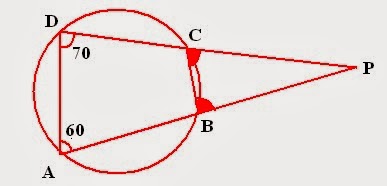
- Cyclic quadrilateral has all its vertices on circle and sum of all angles is
- Sum of opposite angles =
- External angle = Opposite internal angle.
Therefore,
So,
See its very simple question, if you know the properties of geometry. Let's try more examples
Example2: ABCD is a parallelogram and P is any point within it. If area of parallelogram is 20 units, then what will be the sum of areas of triangle PAB and PCD?
Solution: According to the question, figure will be as follows:

Properties for this question:
- Area of parallelogram = Base times Height.
- Area of triangle = 1/2 Base times altitude.
Given that: Area of parallelogram = 20
i.e. Base times Height = 20
To find = Area of ( PAB +PCD)
⇒(1/2)
Example3: ABCD is a cyclic trapezium with AB parallel DC and AB diameter of circle. If
Solution: According to ques, figure will be as follows:
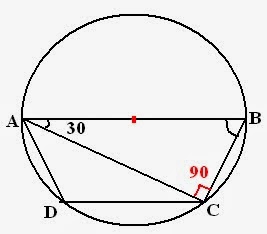
- Angle subtended by diameter is always
- Sum of angles of triangle =
- Sum of opposite angles =
Therefore,
angle
Example4: Two side of plot measures 30m and 22m and angle between them is
Solution: Figure becomes: Center point of BD = O 
ABD is a right angle triangle, therefore, Pythagoras theorem followed.
Given that,
So,
Similarly, using Pythagoras theorem,
Now, Area of triangles
New Questions in High school geometry
The distance between the centers of two circles C1 and C2 is equal to 10 cm. The circles have equal radii of 10 cm.

A part of circumference of a circle is called
A. Radius
B. Segment
C. Arc
D. SectorThe perimeter of a basketball court is 108 meters and the length is 6 meters longer than twice the width. What are the length and width?
What are the coordinates of the center and the length of the radius of the circle represented by the equation ?
Which of the following pairs of angles are supplementary?
128,62
113,47
154,36
108,72What is the surface area to volume ratio of a sphere?
An angle which measures 89 degrees is a/an _____.
right angle
acute angle
obtuse angle
straight angleHerman drew a 4 sided figure which had only one pair of parallel sides. What could this figure be?
Trapezium
Parallelogram
Square
RectangleWhich quadrilateral has: All sides equal, and opposite angles equal?
Trapezium
Rhombus
Kite
RectangleKaren says every equilateral triangle is acute. Is this true?
Find the number of lines of symmetry of a circle.
A. 0
B. 4
C. 2
D. InfiniteThe endpoints of a diameter of a circle are located at (5,9) and (11, 17). What is the equation of the circle?
What is the number of lines of symmetry in a scalene triangle?
A. 0
B. 1
C. 2
D. 3How many diagonals does a rectangle has?
A quadrilateral whose diagonals are unequal, perpendicular and bisect each other is called a.
A. rhombus
B. trapezium
C. parallelogram