Ratio and Proportion
- Some facts of Ratio and proportion
- Ratio is written as 2:3, where 2 and 3 are known as terms.
- First term i.e. 2 is known as Antecedent.
- Second term i.e. 3 is known as Consequent.
- 2^2: 3^2 is known as duplicate ratio of 2:3.
- 2^3:3^3 is known as triplicate ratio of 2:3.
- sqrt2: sqrt3 is sub-duplicate ratio of 2:3.
- a^(1/3) : b^(1/3) is sub-triplicate ratio of 2:3.
Ratio and Proportion Trick
Let me tell you one example which can be solved in 30 sec if you use this trick
Example: If A:B = 3: 4, B: C = 2: 3 and C:D = 5:7, then find A:B:C:D. Solution: General method of solving this question is very lengthy, So let me tell me tell you how can we calculate it easily.
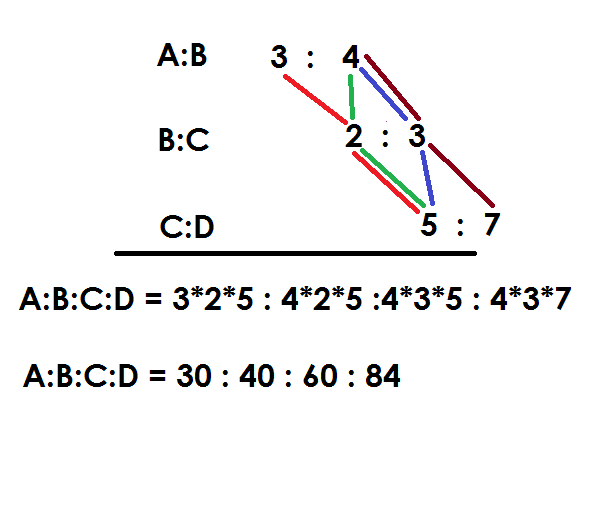
See how it is simple, you just need to remember the pattern and if you notice it, it is really simple . Last and first steps are just the straight lines. So, what is left, just the middle pattern. If I talk about only three terms i.e. A, B and C. Then the pattern will be much easier. Lets see how,
Let us do an example of 5 terms:
Example: If A: B = 3: 4, B: C = 4: 5, C: D = 1: 2 and D: E = 3: 4, Find A: B: C: D: E.
Solution: Similarly, in this case, make the same pattern as in above cases:
Take a pen and try to make it yourself first or do it step by step by looking the solution. then only you can learn this technique.
A: B: C: D: E = 9: 12: 15: 30: 40
So, this is how we solve these types of questions quickly.
I will update one more session of this chapter regarding proportions.
