Divisibility Rules: Quantitative Aptitude Section There are some specific rules by which we can determine the divisor of the given number. Today I wil
Emily-Jane Bray
Answered question
2021-02-26
Answer & Explanation
Ian Adams
Skilled2021-04-16Added 163 answers
Triangles
Triangle = Figure with three sides. Study the following triangle: A,B,C to points. a, b, c to sides. x, y, z to angles.

Perimeter of triangle = a + b + c
Remember that, Sum of all the angles is always
i.e. x + y + z =
Classification of Triangles
Basically there are three types of triangles excluding right angle triangle. Let me tell you how they vary from each other.
- Scalene Triangle
- Isosceles Triangle
- Equilateral Triangle
Scalene Triangle: No side of triangle is equal.
Isosceles Triangle: Two sides of triangle are equal.
Equilateral Triangle: All sides of triangle are equal.
| Scalene | Isosceles | Equilateral | |
| Definition | a ne b ne c | ane b = c | a = b = c |
| Area | A | ||
| Height | - |
where, s = (a+ b+ c)/2
Properties of external angles of Triangle:
1. Sum of all exterior angles is
Study the following set of triangles and their exterior angles,
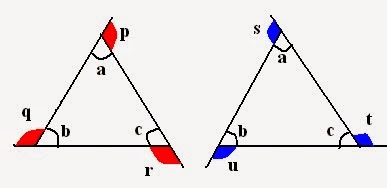
a, b, c to Interior angles. p, q, r and s, t, u to Exterior angles.
So, sum of exterior angles =
2. Next property of exterior angle which is important in paper point of view:
External angle = Sum of two internal angles.
For example: In above figures,
r = a + b
q = a + c
s = b + c and so on.
Right angle Triangle
Following triangle is a right angle triangle i.e. a triangle with one out of three 90^o angle. 
Area of right angle triangle
Area = 1/2 times Base times Perpendicular
Example with Solution
Example: In following figure, CE is perpendicular to AB, angle ACE = 20^o and angle ABD = 50^o. Find angle BDA:
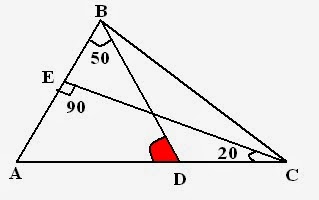
Solution: To Find: angle BDA
For this what we need --- angle BAD Because, Sum of all angles =
Consider, triangle ECA,
CEA + EAC + ACE =
Now, come to triangle ABD,
ABD + BDA + BAD =
Example: In given figure. BC is produced to D and angle BAC =
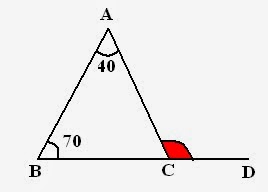
Solution: In above figure, ACD is an exterior angle, and according to property, Exterior angle = Sum of interior angles Therefore, ACD =
This is not the end of this chapter. These are just the basics. In next session, I will discuss some important results, properties (congruency, similarity) and much more. Always remember, Geometry needs practice and time.
New Questions in Algebra II
Which operation could we perform in order to find the number of milliseconds in a year??
Tell about the meaning of Sxx and Sxy in simple linear regression,, especially the meaning of those formulas
Is the number 7356 divisible by 12? Also find the remainder.
A) No
B) 0
C) Yes
D) 6What is a positive integer?
Determine the value of k if the remainder is 3 given
Is a prime number?
What is the square root of ?
Is the sum of two prime numbers is always even?
149600000000 is equal to
A)
B)
C)
D)Find the value of to the base ?
What is the square root of 3 divided by 2 .
write as an equivalent expression using a fractional exponent.
simplify
What is the square root of