Straight Lines Graph the straight lines in Exercises 1–3.Then find the change in y for a one-uni
Lipossig
Answered question
2020-11-29
Straight Lines Graph the straight lines in Exercises 1–3.
Then find the change in y for a one-unit change in x, find the point at which the line crosses the y-axis, and calculate the value of y when x 52.5.
1.
2.
3.
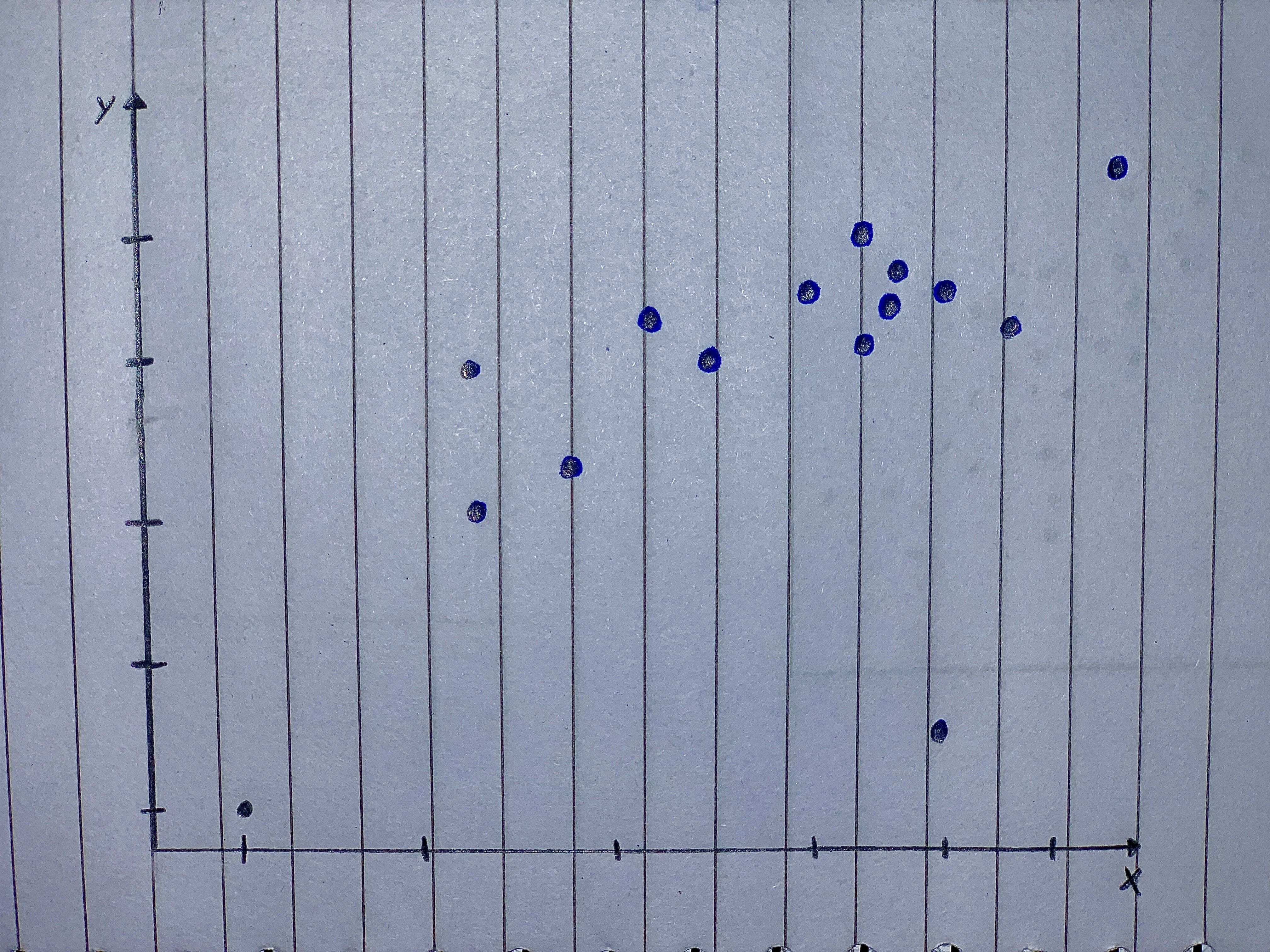
Scatterplots For the scatterplots in Exercises 5 describe the pattern that you see. How strong is the pattern? Do you see any outliers or clusters?
..........................
Answer & Explanation
dessinemoie
Skilled2020-11-30Added 90 answers
From the given graph, it is observed that, as x increases y also increases so the direction of the graph is positive.
The given graph is linear as it does follow a straight line path with respect to two variables of graph.
Step 2
The strength of given graph is stronger as there are good number of samples along the line of curve.
There are two cluster of points at the bottom side of the graph where multiple points exist along the line. There is two outlier points as it appears out of the range of linear pattern in graph.
New Questions in High school statistics
Read carefully and choose only one option
A statistic is an unbiased estimator of a parameter when (a) the statistic is calculated from a random sample. (b) in a single sample, the value of the statistic is equal to the value of the parameter. (c) in many samples, the values of the statistic are very close to the value of the parameter. (d) in many samples, the values of the statistic are centered at the value of the parameter. (e) in many samples, the distribution of the statistic has a shape that is approximately NormalConstruct all random samples consisting three observations from the given data. Arrange the observations in ascending order without replacement and repetition.
86 89 92 95 98.Find the mean of the following data: 12,10,15,10,16,12,10,15,15,13.
The equation has a positive slope and a negativey-intercept.
1) y=−2x−3
2) y=2−3x
3) y=2+3x
4) y=−2+3xWhat term refers to the standard deviation of the sampling distribution?
Fill in the blanks to make the statement true: .
What percent of is
The first 15 digits of pi are as follows: 3.14159265358979
The frequency distribution table for the digits is as follows:
Which two digits appear for 3 times each?
A) 1, 7
B) 2, 6
C) 5, 9<br<D) 3, 8How to write
What is the simple interest of a loan for $1000 with 5 percent interest after 3 years?
What number is 12% of 45?
The probability that an automobile being filled with gasoline also needs an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and the filter need changing is 0.10. (a) If the oil has to be changed, what is the probability that a new oil filter is needed? (b) If a new oil filter is needed, what is the probability that the oil has to be changed?
Leasing a car. The price of the car is$45,000. You have $3000 for a down payment. The term of the lease is and the interest rate is 3.5% APR. The buyout on the lease is51% of its purchase price and it is due at the end of the term. What are the monthly lease payments (before tax)?
The mean of sample A is significantly different than the mean of sample B. Sample A: Sample B: Use a two-tailed -test of independent samples for the above hypothesis and data. What is the -value?
What is mean and its advantages?