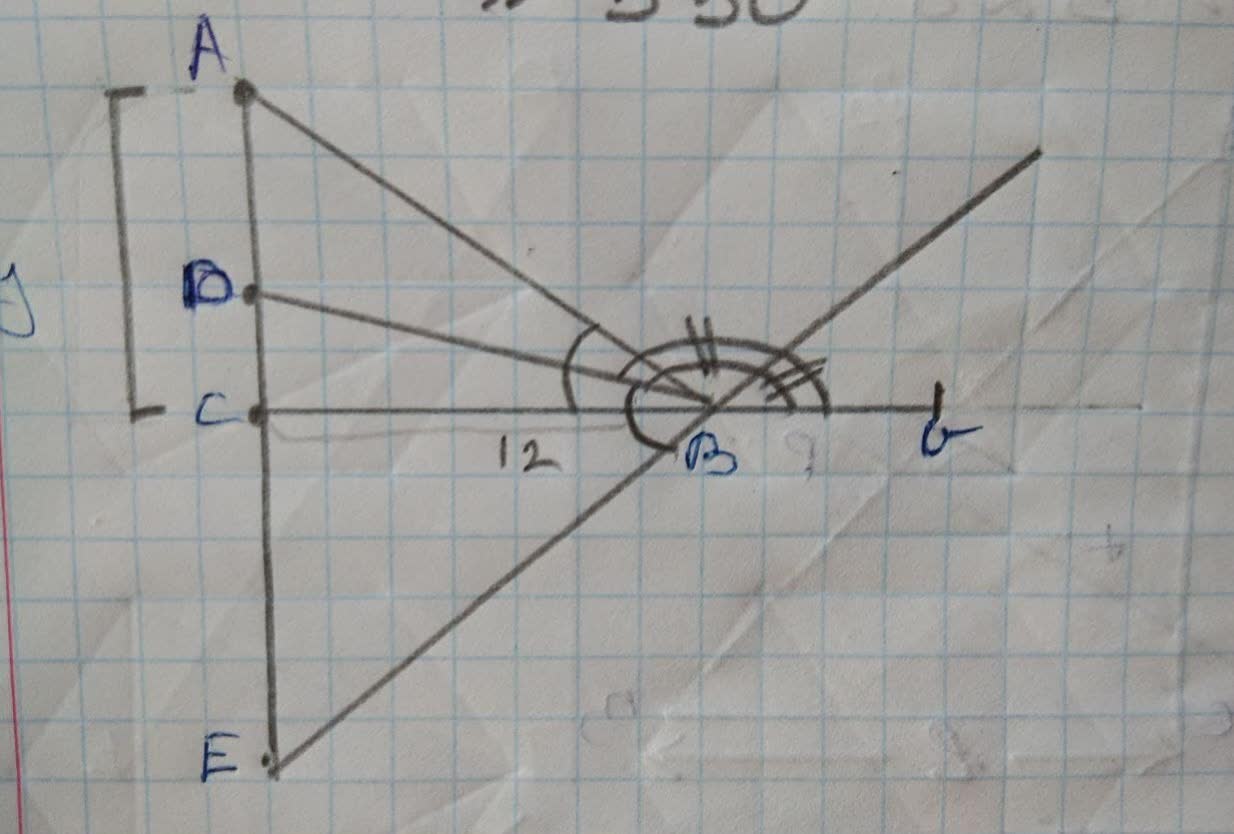
triangle ABC is a right triangle with its right angle at C. The bisector of angle B intersects AC at D. The bisector of the exterior angle at B intersects AC at E. If BD= 15 and BE=20, what are the lengths of triangle ABC?

Question

Marian Tucker · Accepted Answer

Step 1  Using basic properties of triangles we can solve this question.    Step2  angle abc is bisected by bd  angle abg is bisected by be  angle dbe=90(half of a angle in a straight line)  bd=15cm  be=20cm  By pythagoras theorem,  de=25cm  Let de=xcm  be=be2−ce2  =bd2−dc2  =12cm  Step 3  ∠dbc=dcbc  =912  dc=x  ec=25−x  be2−ce2=bd2−x2  x=dc  =9cm  ∠abc=2∠0bc  =247  247=y12  y=24⋆127  ac=2887  By pythagoras theorem  ac2+bc2=ab2  ab=3007

triangle ABC is a right triangle with its right angle

Answered question

Answer & Explanation

New Questions in Trigonometry