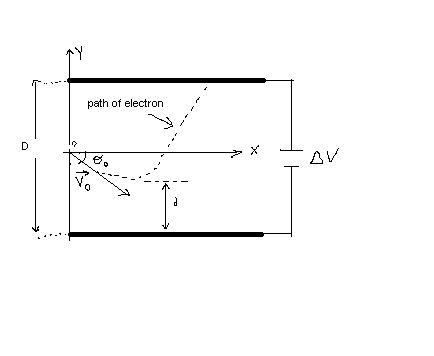
An electron is fired at a speed of v_0 = 5.6\times10^6 m/s and at an angle of \theta_0=–45^\circ between two parallel conductingplates that are D=2.0
Trent Carpenter
Answered question
2021-05-12
An electron is fired at a speed of
Answer & Explanation
Aubree Mcintyre
Skilled2021-05-14Added 73 answers
Initial speed of the electron is
The distance betweeen two parallel conducting plates is
The potential difference between the plates is
Now the direction of the electric field is along the Y-direction.
Now the electric field strength can be calculated by using the formula
The acceleration of the electron is calculated as
(a) The initial velocity v0 can beresolved into two components.
Horizontal component is
Vertical component is
At the bottom plate the final velocity of the electron is zero.
That means
Now the vertical displacement of the electron is calculated byusing the formula
Now the minimum distance above the bottom plate is then
b) The time for electron to travel from the point O to the upperplate is ccalculated as
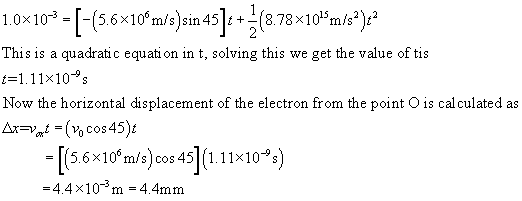
New Questions in Other
22+64
When a cold drink is taken from a refrigerator, its temperature is 5 degree C. After 25 minutes in a 20 degree C room its temperature has increased to 10 degree C. What is the temperature of the drink after 50 minutes?
How many minutes are there in hours?
Find the answer for power .
The following law describes the relationship between gas volume and pressure: ________. A)Boyle's law; B)Henry's law; C)Charles' law; D)Dalton's law
If an electric switch is open then no current flows through the circuit.
A)True;
B)FalseThe price elasticity of supply of a good is 0.8. Its price rises by 50 per cent. Calculate the percentage increase in its supply.
How many quarts are in 10 gallons?
When the net force acting on an object is zero, the total momentum of the system will:
A)remain constant;
B)increase with time;
C)decrease with time;
D)None of theseHow many centimeters are in four meters?
A notebook computer has a mass of 2.25 kilograms. About how many pounds does the notebook weigh?
If the dot product of two non-zero vectors is zero, then the vectors A)are parallel to each other. B)are perpendicular to each other. C)can have any orientation. D)are anti-parallel to each other.
Which is longer 5 miles or 10 kilometers?
9 grams is how many milligrams?
How to write in scientific notation?