A 0.50 kg ball that is tied to the end of a 1.1 m light cord is revolved in a horizontal planewith
Harlen Pritchard
Answered question
2020-11-05
A 0.50 kg ball that is tied to the end of a 1.1 m light cord is revolved in a horizontal planewith the cord making a angle, with the vertical.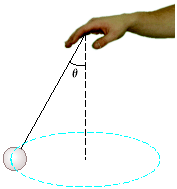
a) Determine the ball speed.
b) If, instead, the ball is revolved so that its speed is 4.0 m/s,what angle does the cord make with the vertical?
c) If the cord can withstand a maximum tension of 9.1 N, what is the highest speed at which the ballcan move?
Answer & Explanation
Aubree Mcintyre
Skilled2020-11-06Added 73 answers
a)
b):
degrees
c):
New Questions in Force, Motion and Energy
Three identical blocks connected by ideal strings are being pulled along a horizontal frictionless surface by a horizontal force The magnitude of the tension in the string between blocks B and C is T=3.00N. Each block has mass m=0.400kg.
What is the magnitude F of the force?
What is the tension in the string between block A and block B??We have: A golf ball of mass 0.045 kg is hit off the tee at a speed of 45 m/s. The golf club was in contact with the ball for s. Find (a) the impulse imparted to the golf ball,and (b) the average force exerted on the ball by the golf club
???A box is sliding with a speed of 4.50 m/s on a horizontal surface when, at point P, it encounters a rough section. On the rough section, the coefficient of friction is not constant but starts at .100 at P and increases linerly with distance past P, reaching a value of .600 at 12.5 m past point P. (a) Use the work energy theorem to find how far this box slides before stopping. (b) What is the coefficient of friction at the stopping point? (c) How far would the box have slid iff the friciton coefficient didn't increase, but instead had the constant value of .1?
?
The spring in the figure (a) is compressed by length delta x . It launches the block across a frictionless surface with speed v0. The two springs in the figure (b) are identical to the spring of the figure (a). They are compressed by the same length delta x and used to launch the same block. What is the block's speed now?A spring gun's spring has a constant force k =400 N/m and negligible mass. The spring is compressed 6.00 cm and a ball with mass 0.0300 kg is placed in the horizontal barrel against the compressed spring.The ball is then launched out of the gun's barrel after the spring is released. The barrel is 6.00 cm long, so the ball leaves the barrel at the same point that it loses contact with the spring. The gun is held so the barrel is horizontal. Calculate the speed with which the ballleaves the barrel if you can ignore friction. Calculate the speed of the ball as it leavesthe barrel if a constant resisting force of 6.00 Nacts on the ball as it moves along the barrel. For the situation in part (b), at what position along the barrel does the ball have the greatest speed?
?A small rock with mass 0.12 kg is fastened to a massless string with length 0.80 m to form a pendulum. The pendulum is swinging so as to make a maximum angle of 45 with the vertical. Air Resistance is negligible.
?
a) What is the speed of the rock when the string passesthrough the vertical position?
b) What is the tension in the string when it makes an angle of 45 with the vertical?
c) What is the tension in the string as it passes through the vertical?
Calculate the actual mechanical advantage of a lever.
The change in internal energy of a system that has absorbed 2 kcal of heat and does 500 J of work is
A) 6400J
B) 5400J
C) 7860J
D) 8900JThe electric field 10 cm from a long wire is 2.4 kN/C. If wire carries uniform charge, what will be the field strength at 40 cm from the wire?
Read each statement below carefully and state, with reasons, if it is true or false : (a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre (b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point (c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector
Two paths lead to the top of a hill. One is shorter and steeper and the second one is longer but less steep. For which of the two paths is the gain in potential energy more?
A) Path I
B) Path II
C) Same for both the paths
D) Data insufficientWhat does negative mean?
What is a lever.
The gravitational unit of force is_?
What do you mean by ?