The figure shows the surface created when the cylinder y^2+Z^2=1 intersects the cylinder x^2+Z^2=1. Find the area of this surface.The figure is something like:FSP02510400011.jpgFSZ
sodni3
Answered question
2020-12-16
The figure shows the surface created when the cylinder intersects the cylinder . Find the area of this surface.
The figure is below: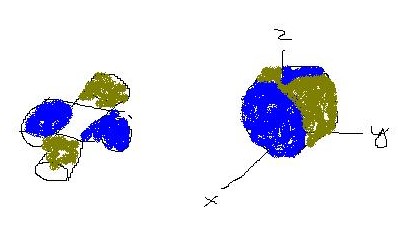
Answer & Explanation
stuth1
Skilled2020-12-17Added 97 answers
Note that the given cylinder will intersect at four congruent surfaces. e. equal in area. We need to find the area of only one side and then multiply it by 4.
First, we find the area of the face of the surface that intersect the positive y axis. The surface is located above the area. then
Consequently, the sum of the areas of the intersecting surface is
New Questions in High School
At the beginning of an environmental study, ad forest covered an area of .Since then, this area has decreased by 4.25% each year.Let t be the number of years since the start of the study.Let y be the area that the forest covers in .
Write an exponential function showing relationship between y and t.Some friends tell you that they paid $25,000 down on a new house and are to pay $525 per month for 30 years. If interest is 7.8% compounded monthly, what was the selling price of the house? How much interest will they pay in 30 years?
t e^-4t sin3t
Find all whole number solutions of the congruence equation.
3x ≡ 8 mod 11Use a direct proof to show that the product of two rational numbers is rational.

Y=2(x-) (x+1)
what is vertex
axis of symmetry
x-intercept(s)
y-intercept
Stairs- Each step of a set of stairs has a tread depth of 11.5 inches and a riser height of 6.5 inches. What is the slope of the set of stairs?
A ball of mass 5 kg is attached to a string of length 10 cm, forming a pendulum. If the string is raised horizontally as shown and released from point A, then what is the v
assume that the random variable Xand Y have the joint pdf f(x,y)=1/2x^3
5=20 mod 4 true or false answer
5x−4y=
- −12
Pets Plus and Pet Planet are having a sale on the same aquarium. At Pets Plus the aquarium is on sale for 30% off the original price and at Pet Planet it is discounted by 25%.
Store Original Price
of Aquarium ($)Pets Plus 118 Pet Planet 110 If the sales tax rate is 8%, which store has the lower sale price?
, 1 of 1.Select ChoicePets PlusPet Planet has the lower sale price.
Part B
Fill in the blank question.
How much will you save by buying the aquarium at the store with the lower sale price? Round to the nearest cent.
$
Prove that if x is and irrational number and x>0 then route over x is also irrational
A small object has charge Q. Charge q is removed from it and placed on a second small object. The two objects are placed 1 m apart. For the force that each object exerts on the other to be a maximum. q should be: A. 2Q B. Q C. Q/2 D. Q/4 E. 0